ต้องใช้จำนวนสิ่งตัวอย่างเท่าไหร่ ถ้าต้องการความมั่นใจ 95% เพื่อบอกว่าผลิตภัณฑ์เป็นของดีอย่างน้อย 95% หรือ 99%
คำตอบที่จะได้ขึ้นกับว่าค่าตัวแปรตอบสนองนั้นเป็นค่านับหรือค่าวัด(ข้อมูลแบบต่อเนื่อง) จะทำให้รูปแบบการสุ่มตัวอย่างนั้นเปลี่ยนไป โดยการสุ่มตัวอย่างมี 2 แบบ คือ
การสุ่มตัวอย่างเชิงคุณลักษณะสามารถใช้ได้กับทุกกรณีไม่ว่าข้อมูลจะมีการแจกแจงแบบใด แต่การสุ่มตัวอย่างแบบผันแปรข้อมูลจะต้องมีการแจกแจงแบบปกติ แต่อาจจะใช้จำนวนสิ่งตัวอย่างน้อยกว่าแบบเชิงคุณลักษณะ
ในบทความนี้จะเน้นไปที่ข้อมูลเชิงคุณลักษณะ
การสุ่มตัวอย่างเชิงคุณลักษณะ (Attribute Sampling)
สูตรที่ใช้คำนวณหาจำนวนสิ่งตัวอย่างเพื่อให้ได้ ความเชื่อมั่น 95% คือ 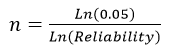
โดยค่า คือ ค่าความน่าจะเป็นที่ชิ้นงานหรือผลลัพธ์อยู่ในข้อกำหนดเฉพาะ หรืออีกนัยหนึ่ง คือ จำนวนชิ้นงาน n ชิ้นนี้มีข้อบกพร่องเป็นศูนย์
ตัวอย่างเช่น
ความน่าเชื่อถือ (reliability) เท่ากับ 0.95 หรือ 95% จำนวนสิ่งตัวอย่างที่ต้องใช้ คือ 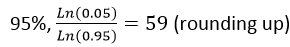 (ปัดเศษขึ้น)
(ปัดเศษขึ้น)
ความน่าเชื่อถือ (reliability) เท่ากับ 0.99 หรือ 99% จำนวนสิ่งตัวอย่างที่ต้องใช้ คือ  (ปัดเศษขึ้น)
(ปัดเศษขึ้น)
Minitab สามารถหาค่า n นี้ได้เช่นกันโดยใช้คำสั่ง Stat > Basic Statistics > 1 Proportion
โดยจะต้องใส่ค่าพารามิเตอร์เพื่อให้ Minitab ทำการประมวลค่าจำนวนสิ่งตัวอย่างตามระดับความน่าเชื่อถือที่ต้องการ ตามที่แสดงในรูปด้านล่างนี้
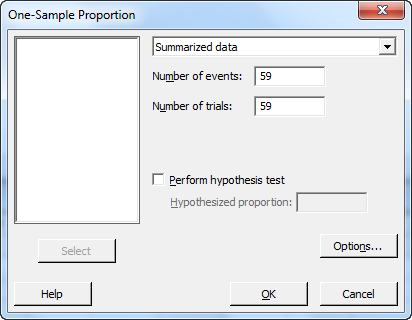

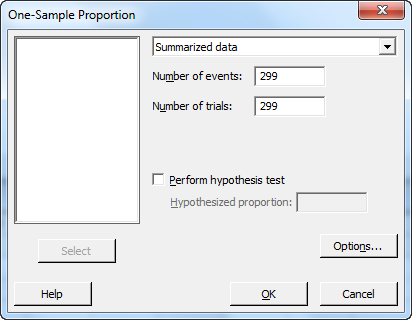

แผนการชักสิ่งตัวอย่างที่ได้มาทั้งสองแผนนี้จะใช้สำหรับกรณีที่ ขนาดลอตแบบไม่จำกัด(infinite lot size) และจำนวนเพื่อการยอมรับ (acceptance number, C) เท่ากับศูนย์ (C=0)
ซึ่งการสร้างแผนการชักสิ่งตัวอย่างสามารถใช้คำสั่ง Stat > Quality Tools > Acceptance Sampling by Attributes ซึ่งสามารถกำหนดค่าพารามิเตอร์ได้ตามนี้
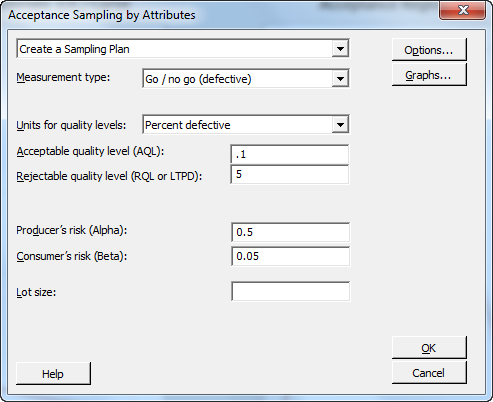
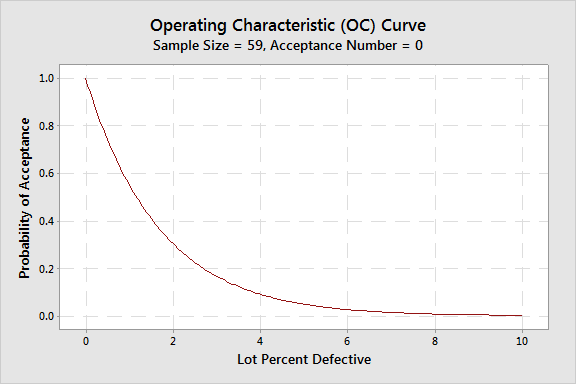
ถ้าเปลี่ยน RQL เป็น 1% จะได้แผนการชักสิ่งตัวอย่าง C=0 ได้ตามนี้
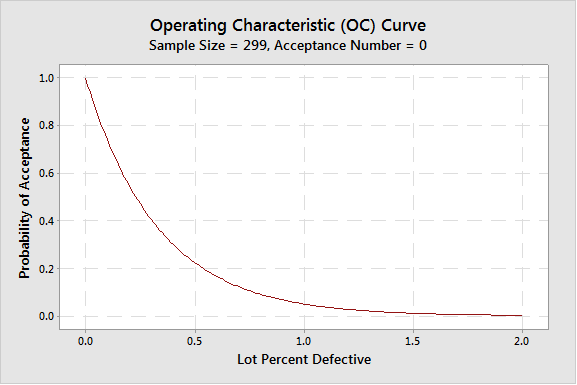
ถ้าคุณต้องการระดับความเชื่อมั่นเท่าเดิม แต่ยอมให้มีชิ้นงานบกพร่องเกิดขึ้นในการตรวจสอบได้ 1 ชิ้น (C=1) จำนวนสิ่งตัวอย่างที่ต้องสุ่มมาจะต้องมีจำนวนมากขึ้น เช่น ถ้ายอมให้ชิ้นงานบกพร่องในการตรวจสอบได้ 1 ชิ้น สิ่งตัวอย่างที่ต้องสุ่มมาคือ 93 ด้วยระดับความเชื่อมั่น 95%
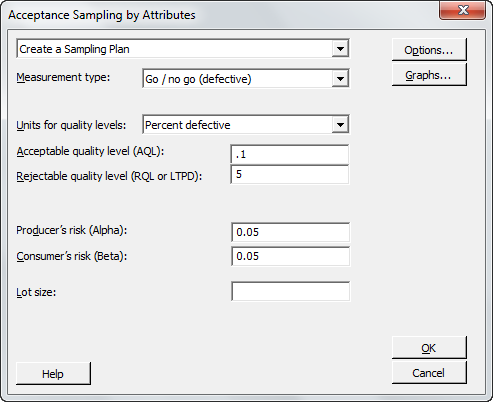
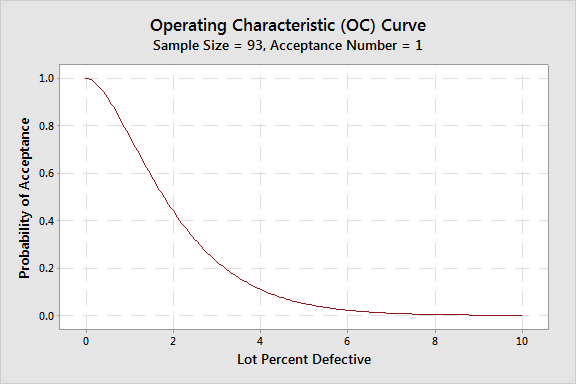
รูปด้านบน คือ แผนการชักสิ่งตัวอย่างที่ใช้ C = 1 และมีความเสี่ยงของผู้ผลิตเท่ากับ 0.05
จากที่กล่าวมาทั้งหมดจะเห็นว่าถ้ากำหนดให้จำนวนเพื่อการยอมรับ (acceptance number)เท่ากับศูนย์ จะใช้จำนวนสิ่งตัวอย่างที่น้อยกว่ามาก และเมื่อเพิ่มค่าจำนวนเพื่อการยอมรับจาก 0 ไปเป็น 1 จะต้องใช้สิ่งตัวอย่างเพิ่มขึ้นจาก 59 ไปเป็น 93
บทความต้นฉบับ : https://blog.minitab.com/blog/the-statistical-mentor/how-many-samples-do-you-need-to-be-confident-your-product-is-good
เนื้อหาบทความโดยบริษัท Minitab Inc. ประเทศสหรัฐอเมริกา
แปลและเรียบเรียงโดยสุวดี นําพาเจริญ และ ชลทิขา จํารัสพร, บริษัท โซลูชั่น เซ็นเตอร์ จํากัด webadmin@solutioncenterminitab.com
บทความนี้เกิดจากการเขียนและส่งขึ้นมาสู่ระบบแบบอัตโนมัติ สมาคมฯไม่รับผิดชอบต่อบทความหรือข้อความใดๆ ทั้งสิ้น เพราะไม่สามารถระบุได้ว่าเป็นความจริงหรือไม่ ผู้อ่านจึงควรใช้วิจารณญาณในการกลั่นกรอง และหากท่านพบเห็นข้อความใดที่ขัดต่อกฎหมายและศีลธรรม หรือทำให้เกิดความเสียหาย หรือละเมิดสิทธิใดๆ กรุณาแจ้งมาที่ ht.ro.apt@ecivres-bew เพื่อทีมงานจะได้ดำเนินการลบออกจากระบบในทันที